Forming a Magic Square
알고리즘 공부를 해야지 해야지 생각만 하다가 드디어 시작하게 되었습니다. (놀랍게도 학생때부터 지금까지 단한번도 알고리즘 사이트에서 문제를 풀어본 적이 없습니다. = 알고리즘 알못(취직한게 신기할정도))
백준, 코딜리티, 알고스팟 등 여러 알고리즘 풀이 사이트가 있는데 저는 HackerRank로 선택! HackerRank는 문제가 전부 영어로 되어있으며 Java, Kotlin, Swift, Python 등 다양한 언어를 지원합니다.
그래도 경력(?)이 있는데 하며 DIFFICULTY = Medium 을 선택해서 한문제를 풀어봤는데.. 결론은 ‘생각보다 너무 어려운데 ㅋㅋㅋㅋ’와 ‘집중력 최고조에 도달할만큼 너무 재밌다’ 였습니다. 앞으로 꾸준히 풀어보면서 포스팅하려고 합니다!
문제
링크: Forming a Magic Square (Medium Level)
input 값으로 들어온 3x3 행렬을
5 3 4
1 5 8
6 4 2
3x3 Magic Sqaure로 변환한 후
8 3 4
1 5 9
6 7 2
두 행렬의 차의 합을 구했을 시 가장 작은 값을 구하는 문제입니다.
|5-8| + |8-9| + |4-7| = 7
풀이
홀수 마방진
우선 Magic Square가 무엇인지 알아야 합니다. Magic Square는 흔히 마방진으로 알려져 있으며 가로, 세로, 대각선의 합이 모두 같은 정사각형 배열을 의미합니다. 3방진의 경우 가로, 세로, 대각선의 합이 15입니다.
마방진은 만드는 규칙이 있습니다. 홀수 배열 마방진과 짝수 배열 마방진은 그 규칙이 조금 다른데 이 포스트 에서는 홀수 마방진을 만드는 방법만 설명합니다.
(이해하기 쉽게 그림을 그려보았습니다. 잘 그린 것 같아서 뿌듯합니다.ㅎㅅㅎ)
1. 정사각형 맨 윗줄 가운데에 1을 적습니다.
2. 오른쪽 대각선 방향에 다음 숫자를 적습니다.
(정사각형 영역 밖인 경우 수직 또는 수평으로 이동합니다.)
3. 다음 칸에 이미 숫자가 존재하는 경우 아랫칸에 다음 숫자를 적습니다.
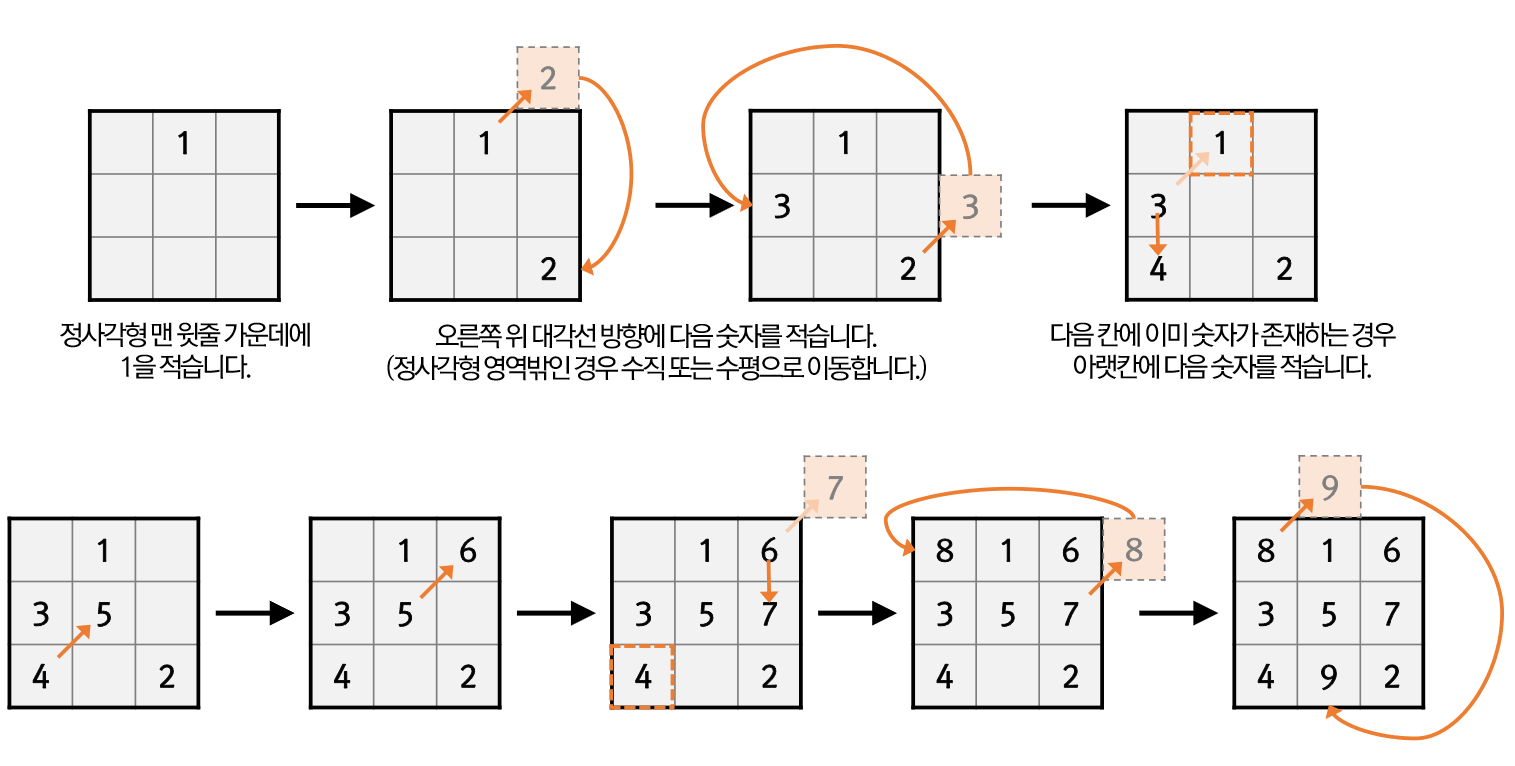
중학교 수학 짜투리시간에 마방진 만드는 법을 배웠어서 저는 비교적 문제풀기가 쉬웠습니다. (숫자 1의 위치를 맨아랫줄 가운데로 해도 상관없으며 대각선 방향 등 약간씩 풀이가 달라도 결국 해당 마방진이 회전됐을 뿐 숫자배열은 같음(…))
- 3차 행렬 만들기
- 사실 3차 Magic Square의 경우 4개의 모서리는 {2, 4, 6, 8}로 들어가며 가운데는 무조건 숫자 {5}, 그 외에는 {1, 3, 5, 7} 이 들어가게 되는데, 간단하게 로직을 짜기 위해 가운데 5만 고정값으로 생각하였습니다. 가운데 5를 제외한 {1, 2, 3, 4, 6, 7, 8, 9}의 조합으로 나올 수 있는 행렬의 갯수는 8! 입니다.
- perm 함수를 이용해서 {1, 2, 3, 4, 6, 7, 8, 9}의 조합으로 나올 수 있는 행렬을 모두 만들었습니다.
static void perm(List<List<Integer>> permList, int[] arr, int pivot) {
if (pivot == arr.length) {
List<Integer> a = new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
a.add(arr[i]);
}
permList.add(a);
return;
}
for (int i = pivot; i < arr.length; i++) {
swap(arr, i, pivot);
perm(permList, arr, pivot + 1);
swap(arr, i, pivot);
}
}
static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
- 3차 Magic Square 만들기
- makeMagicSquare() 함수를 통해 Magic Square의 규칙인 ‘가로, 세로, 대각선의 합이 15’인 행렬만 추가하여 총 8개의 Magic Square를 만듭니다.
static List<List<Integer>> makeMagicSquare() {
//가운데 5는 고정, 8개의 숫자순열
int arr[] = {1, 2, 3, 4, 6, 7, 8, 9};
List<List<Integer>> permList = new ArrayList<>();
perm(permList, arr, 0);
for (List<Integer> a : permList) {
a.add(4, 5);
}
//가로, 세로, 대각선 합이 15인 행렬만 추가
List<List<Integer>> magicSquare = new ArrayList<>();
for (List<Integer> a : permList) {
if ((a.get(0) + a.get(1) + a.get(2)) == 15 &&
(a.get(3) + a.get(4) + a.get(5)) == 15 &&
(a.get(6) + a.get(7) + a.get(8)) == 15 &&
(a.get(0) + a.get(3) + a.get(6)) == 15 &&
(a.get(1) + a.get(4) + a.get(7)) == 15 &&
(a.get(2) + a.get(5) + a.get(8)) == 15 &&
(a.get(0) + a.get(4) + a.get(8)) == 15 &&
(a.get(2) + a.get(4) + a.get(6)) == 15) {
magicSquare.add(a);
}
}
return magicSquare;
}
- input 행렬과의 차의 합을 구했을 때 가장 작은 값
- 2에서 구한 Magic Square의 갯수만큼 for문을 돌아 minCost를 구합니다.
- 모든 차이가 가장 작은 1과 가장 큰 9의 차인 8만큼 난다고 가정했을 때 가장 큰 값은 72가 나오게 됩니다. minCost = 72로 두고 시작하였습니다.
static int formingMagicSquare(int[][] s) {
//3x3 마방진의 갯수는?
//8 1 6
//3 5 7
//4 9 2
int minCost = 72;
List<List<Integer>> magicSquare = makeMagicSquare();
for (List<Integer> square : magicSquare) {
int cost = 0;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cost += Math.abs(s[i][j] - square.remove(0));
}
}
if (cost < minCost) {
minCost = cost;
}
}
return minCost;
}
위 풀이로 모든 테스트케이스를 패스하였습니다!
전체코드는 Github에서 확인할 수 있습니다.
(개인적인 풀이방식이며 더 좋은 방법이나 아이디어는 언제든 댓글 달아주세요~)
댓글남기기